※ 주의 ※ 학습하는 과정에서 정리한 글이다보니 부족함이나 오개념이 왕왕 있을 수 있습니다. 읽더라도 참고만 하시고 교차 검증하시길 바라고.. 틀린 개념이 있다면 알려주시면 감사히 수정하겠습니다.
선형대수학의 개념
학부 1학년 때 공대 애들을 만나면 선형대수학이라는 걸 공부하고 있다고 종종 들었다. 그때마다 ‘아니 수학이면 수학이지 선형이 뭔데…’라는 생각을 했다. 궁금해서 찾아보긴 했으나 이해도 안가고 결국 포기했던 것 같다.
하지만 다시 해야하죠?
나름 유튜브와 구글링을 통해 알게된 선형대수학의 기본 개념을 정리해보려고 한다.
수학
뜬금없지만 수학에 대한 정리도 해보겠다. 갑자기 궁금하길래… 아무튼 수학은 “수와 도형, 그리고 이에 대한 연산에 대한 학문”이다. 기본적으로 수학의 여러 분야들이 공통적으로 “대상과 연산”으로 구성된다고 한다.
선형대수학
선형대수학은 “벡터와 행렬 및 이에 대한 연산에 대한 학문”이다. 선형대수학은 매우 매우 중요한 학문이라 공대에서는 거의 필수적으로 듣는 듯하다.
선형대수학은 대수학(Algebra)에 속하는데, 그럼 대수학은 뭘까? 대수학의 ‘대’는 한자어로 큰 대 자가 아니라, 대신한다 할 때 그 대 자라고 한다. 즉, 숫자 대신 문자를 사용한다는 건데, 우리가 아는 방정식(x^2+ 5x + 4 = 0)이 대표적이다. (엄밀히는 대수적 구조에 대한 학문이라는데 대수적 구조가 뭔지 모르겠다…)
한편 선형(Linear)라는 말은 그냥 선 형태가 아니라, ‘직선 형태’라는 뜻이다. 따라서 2차 방정식은 곡선이니까 선형이 아니고, 1차 방정식이 직선이므로 선형 방정식이 된다. (나중 가면 직선이 아닌 선형도 있다고 하는데 그때는 ‘결과가 예측된다’는 의미의 선형으로 사용된다나…)
종합적으로 보면 선형(Linear) 대수학(Algebra)는 선형의 1차 방정식을 다루는 학문이다. 이때 단순히 하나의 방정식을 다루지 않고 여러 개의 ‘연립 1차 방정식’을 다루게 된다. 애초에 선형대수학은 연립방정식을 연구하다가 나타났다고 한다.
행렬과 벡터
이때 이러한 선형대수학의 연립 방정식을 사각형 데이터로 단순화할 수 있는데, 그게 바로 ‘행렬과 백터’다. 예를 들어보자.
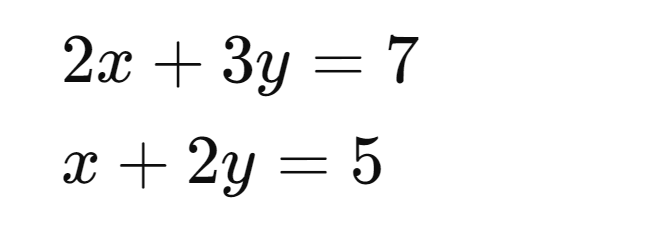
뭐 이런 연립 방정식이 있다고 해보자. 차수가 1이니까 선형 방정식이라 할 수 있다. 이때, 위 연립 방정식을 아래와 같이 단순화 할 수 있다.
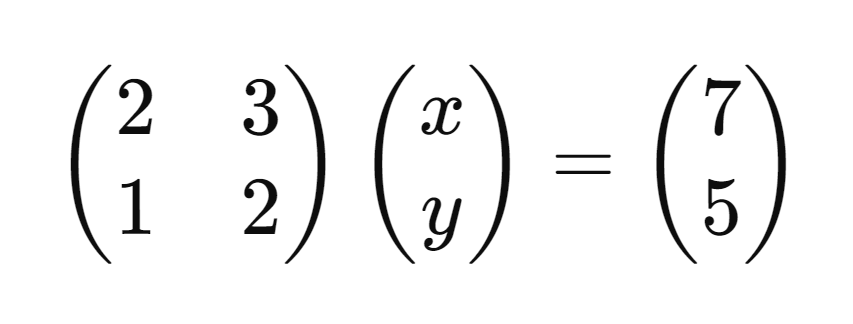
이때 이렇게 사각형 모양으로 가로 세로 숫자를 나열한 것을 행렬이라고 하고, 위 사진의 x y나 7 5 처럼 한 줄로 숫자를 늘어 놓은 것을 벡터라고 한다. 이때 숫자가 세로로 나열되어 있다면 열벡터라고 하고, 가로로 나열되어 있다면 행벡터 라고 한다. 근데 보통 열벡터를 쓴다.
벡터는 엄밀히 ‘벡터 공간의 원소’를 의미하지만, 이러한 의미 외에도 물리학에서 추가적인 의미로 사용된다. 이때 벡터는 ‘크기와 방향이 있는 물리량’을 말한다. 대표적으로 속도나 힘이 있다.
스칼라
한편 스칼라라는 개념도 벡터와 함께 많이 사용된다. 스칼라는 크기와 방향이 모두 있는 벡터와 다르게 ‘크기’만 가진 물리량을 말한다. 예를 들어 ‘온도’가 있다. 선형대수학에서 스칼라는 벡터나 행렬에 곱해지는 실수나 복소수를 의미한다.
No Responses